HUFFMAN Algorithm and its implementation in C

Huffman trees are used as message encoding and message decoding trees which is the basic construct of compression and de. The specialty of Huffman tree is that –

• it helps to reduce the bit codes of each symbol in the message according to their relative frequency of occurrence.
• the same tree constructed could be used for both encoding and decoding purposes

How message is encoded or decoded from a Huffman Tree

Consider the following Huffman Tree which uses the symbols AEIOULSTHVJ. Let the relative frequencies of the characters be 10, 3, 5, 8, 10, 20, 6, 15, 7, 6, 2.

The core data-structure in a Huffman tree is a binary tree. As for the above example, the binary tree could be constructed as below –

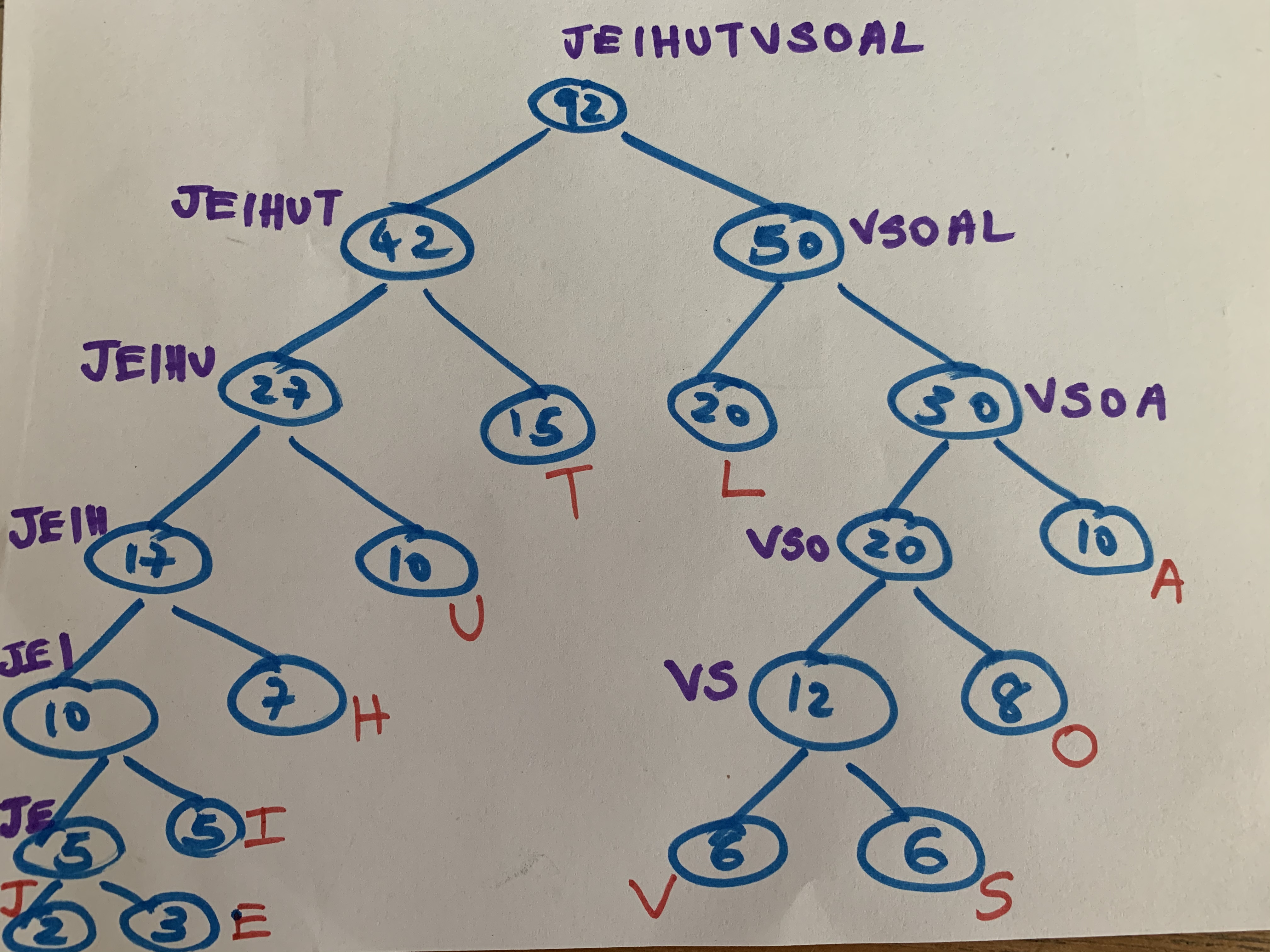
Note how the characters involved in coding/decoding are represented as leaf nodes where the nodes value represents their relative frequency. The root node or the father represents the cumulative frequencies of its leaf nodes.

Suppose we want to encode the code of symbol E. Now start from leaf E and travel up-to the root, write the code from left to right such that code =0 if a left branch is climbed and code = 1 if a right branch is climbed. The codes are read from right to left as we read binary.

Thus, code for E = 000001 (eg: We climb the right branch (1) where E is, reach 5 and traverse up 5 left branches (00000) until we reach the root)

Similarly, code for L = 10

From the coding bit that we arrive at above, we can note that the relative frequency of E (3) is very small when compared with that of L(20).

The above tree could also be used  to decode a code say |1000|100|1011|10|01|. While decoding, we start from the root and descend. The conditions are similar to when we code. i.e. 0 -> when we climb down left branch and 1-> when we climb down a right branch till we reach a leaf and repeat the same process until end of code. In the above case, if we start reading the code from right to left – 01 stand for L since 1 means we descend to the right branch of root and then descend left and reach L. In the same fashion, if we decode the other chunks of the code, it becomes LTOUH.

C Algorithm

We generally use the dynamic representation of Binary Trees to construct the Huffman Tree. We use functions maketree(x), setleft(p,x,), setright(p,x,), setfather(p,p1,p2), isleft(p) and father(p) related to Binary Tree data structure. We also use pqinsert(rootnodes,p) and pqmindelte(rootnodes) related to an ascending priority queue (pq) data structure. Frequencies of each symbol is stored in an array Frequency[i] and code bits in an array Code[i] and an array position[i] to store the positions of nodes pointed by a pointer p in relation to the i^th symbol. The ascending priority queue contains pointers to various nodes and is ordered by p->info of each pointer to a node.

Below is a simple C program to represent a Huffman Tree –

/*initializes set of rootnodes*/

rootnodes = empty ascending priority queue;

/*number of symbols*/

scanf("%d",&n);
/*scans frequency of each symbol*/

scanf("%d",&frequency[i]);
/*inserts pointers to lead containing frequency of a symbol to a pq*/

for(i = 0; i < n; i++){
     p= maketree(frequency[i]);
     position[i] = p;
     pqinsert(rootnodes,p);
}

/*constructs the Huffman Tree*/
while(more than 1 item in the priority queue){
     p1 = pqmindelete(rootnodes);
     p2 = pqmindelete(rootnodes); 
     p  = maketree(info(p1) + info(p2));

     setleft(p,p1);
     setright(p,p2);
     setfather(p,p1,p2);
     pqinsert(rootnodes,p);
}

/*initializes root to root node*/
root = pqmindelete(rootnode);

/*starting from each symbol, travel to root to encode each symbol*/
for(i = 0; i < n; i++){
     p = position[i];
     code[i] = 0;  /*initialized to 0*/
     while(p != root){
         if(isleft{p}){
             code[i] = 0;
             i++;
         }
         else{
             code[i] = 1;
             i++;
         }
         p = father{p);
     }
     /*print code[i] for each symbol*/
}