Representing Graphs and Networks in C

A Graph is a data structure that consists of a set of nodes interconnected by directed or un-directed arcs. For a DIRECTED Graph, the ordered pair of nodes are written within angled brackets while for a UN-DIRECTED Graph, they are written within parenthesis. Consider a directed graph as depicted below –

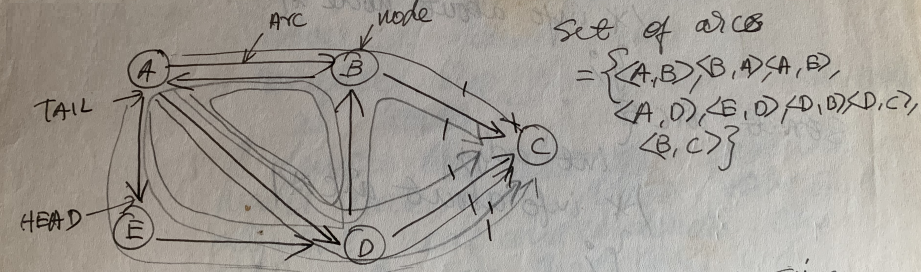
Below are the main point to note about the above graph –

• NODE B is said to be ADJACENT to A since there is an arc from A to B.
• INDEGREE – Number of arcs incident to a node. eg: indegree of B is 2
• OUTDEGREE – Number of arcs incident from a node. eg: outdegree of A is
• Now there are 2 CYCLES from from A to A – 1 from E to E, 2 from D to D and 2 from B to B.
• PATHS from node A to D is of length 1 and length 2
• There are 6 paths from A to C of lengths 2, 2, 3, 3, 6, 6 respectively.

Consider a RELATION, R = {<3,10>, <5,6>, <5,8>, <6,17>, <8,17>, <10,17>}. This relation could  be represented as a WEIGHTED GRAPH or a NETWORK as shown below –

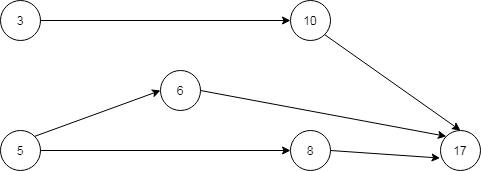
The weight of each arc is 1 which is value of rem(predecessor node/successor node). Relation is {(x,y) / y > x and rem. of y/x is 1}.

General sequential representation of Graphs in C

Below is a complete sequential representation of graphs in C. It is assumed that nodes have data and arcs are weighted.

# define MAXNODES 50
/*Declaration*/
struct node {
             int info;
            };
struct arc {
             int adj;
             int weight;
            };
struct graph {
             struct node nodes[MAXNODES];
             struct arc arcs[MAXNODES][MAXNODES];
            }g;
/*Routine to add information to a node*/
void addinfo(struct graph g, int inf, int node1){
g.nodes[node1].info = inf;
return;
}/*end addinfo*/

/*Routine to join a weighted arc from node 1 to node 2*/
void joinwt(struct graph g, int node1, int node2, int Wt){
g.arcs[node1][node2].adj = TRUE;
g.arcs[node1][node2].weight = Wt;
}/*end joinwt*/

/*Routine to remove an arc*/
void remove(struct graph g, int node1, int node2){
g.arcs[node1][node2].adj = FALSE;
g.arcs[node1][node2].weight = NULL;
}/*end remove*/

/*Routine to check for adjacency*/
void adjacent(struct graph g, int node1, int node2){
return((g.arcs[node1][node2].adj == TRUE) ? TRUE : FALSE);
g.arcs[node1][node2].weight = NULL;
}/*end adjacent*/

In the sequential representation above, nodes and the information associated with them are stored in an array nodes[]. The ADJACENCY  or arcs are created or removed between two nodes i and j using 2D array g.arcs[i][j] where g.arcs[i][j].adj represents the adjacency (arc) and g.arcs[i][j] weight gives the associated weight. g.arcs[i][j] is calles the ADJACENCY MATRIX of order (MAXNODES – 1) x (MAXNODES – 1).

TRANSITIVE CLOSURE – PATH MATRIX of length n 

If we consider that a graph is totally defined by the adjacency matrix such that the nodes have no info field and arcs are not weighted where Adjacency Matrix  a_ij is defined as –

a_ij = { 1, if there exists an adjacency or arc between two nodes i and j.

0, otherwise

}

For such graphs, we use the TRANSITIVE PROPERTY OF GRAPHS to check for the path between two nodes. Consider a graph completely represented as an adjacency matrix.

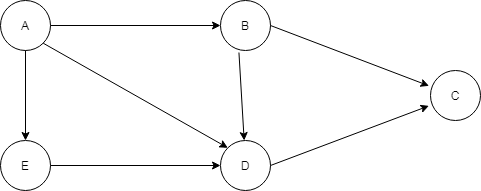
Now the adjacency matrix adj could be written as –

Likewise we could obtain the path matrices upto k where k is the max number of nodes from the boolean product of path matrix of length k-1 and adj.

Matrix Path or Transitive Closure = adj || adj2 || adj3 || ………………….. || adjk

Such a matrix path is often called the  Transitive Closure  of adj matrix. For the above gaph, the transitive closure is –

Transitive Closure (Matrix Path) = adj || adj2 || adj3 || adj4 || adj5 (k=5)

Complete Adjacency Matrix representation of Graphs in C

In such a case, we consider that the nodes have no info associated with it and arcs have no weights associated with them.

Arcs with no weights

# define MAXNODES 50
/*Declaration*/
int adj[MAXNODES][MAXNODES];

/*Routine joining arcs*/
void join(int adj[][MAXNODES], int node1, int node2){
          adj[node1][node2] = TRUE;
}/*end join*/

/*Routine for removing arcs*/
void remove(int adj[][MAXNODES], int node1, int node2){
         adj[node1][node2] = FALSE;
}/*end remove*/

/*Routine to check for adjacency*/
void adjacent(int adj[][MAXNODES], int node1, int node2){
     return((adj[node1][node2] == TRUE) ? TRUE : FALSE);
}/*end adjacent*/

Arcs with weights

# define MAXNODES 50
struct arc {
             int adj;
             int weight;
            };

/*Declaration*/
struct arc g[MAXNODES][MAXNODES];

/*Routine to join a weighted arc from node 1 to node 2*/
void joinwt(struct g[MAXNODES][MAXNODES], int node1, int node2, int Wt){
       g[node1][node2].adj = TRUE;
       g[node1][node2].weight = Wt;
}/*end joinwt*/

/*Routine to remove an arc*/
void remove(struct g[MAXNODES][MAXNODES], int node1, int node2){
       g[node1][node2].adj = FALSE;
       g[node1][node2].weight = NULL;
}/*end remove*