Game Trees

Game Tree is one of the applications of Binary Trees. For example the one implemented for the Tic-Tac-Toe Game.

X | X | X
O | O |    
O |   |

The game is between two players who makes moves ‘X’ and ‘O’ on a board of 3×3 positions. The players who wins is the one who completes a row, col, or diagonal first as shown. Here, the players with ‘X’ wins.

Evaluation Function

Evaluation function for the Game Tree evaluates a static Board position. It is calculated as the number of rows, columns and diagonals left open for a player ‘*’ – the same left of this opponent ‘-‘. It shows how good a position seems to be for a particular player. A MAX evaluation function may be favorable for a maximizing player say ‘+’ and a min value for evaluation function would be favorable for a minimizing player say ‘-‘.

Look Ahead Level 

Suppose it were possible to predict the moves resulting from a board position then the move could be improved considerably. Look ahead level could be defined as the number of future moves to be considered. Starting from any board position, a tree could be constructed for the board positions resulting from each move. Such a Binary Tree is called a Game Tree.

Constructing a Game Tree

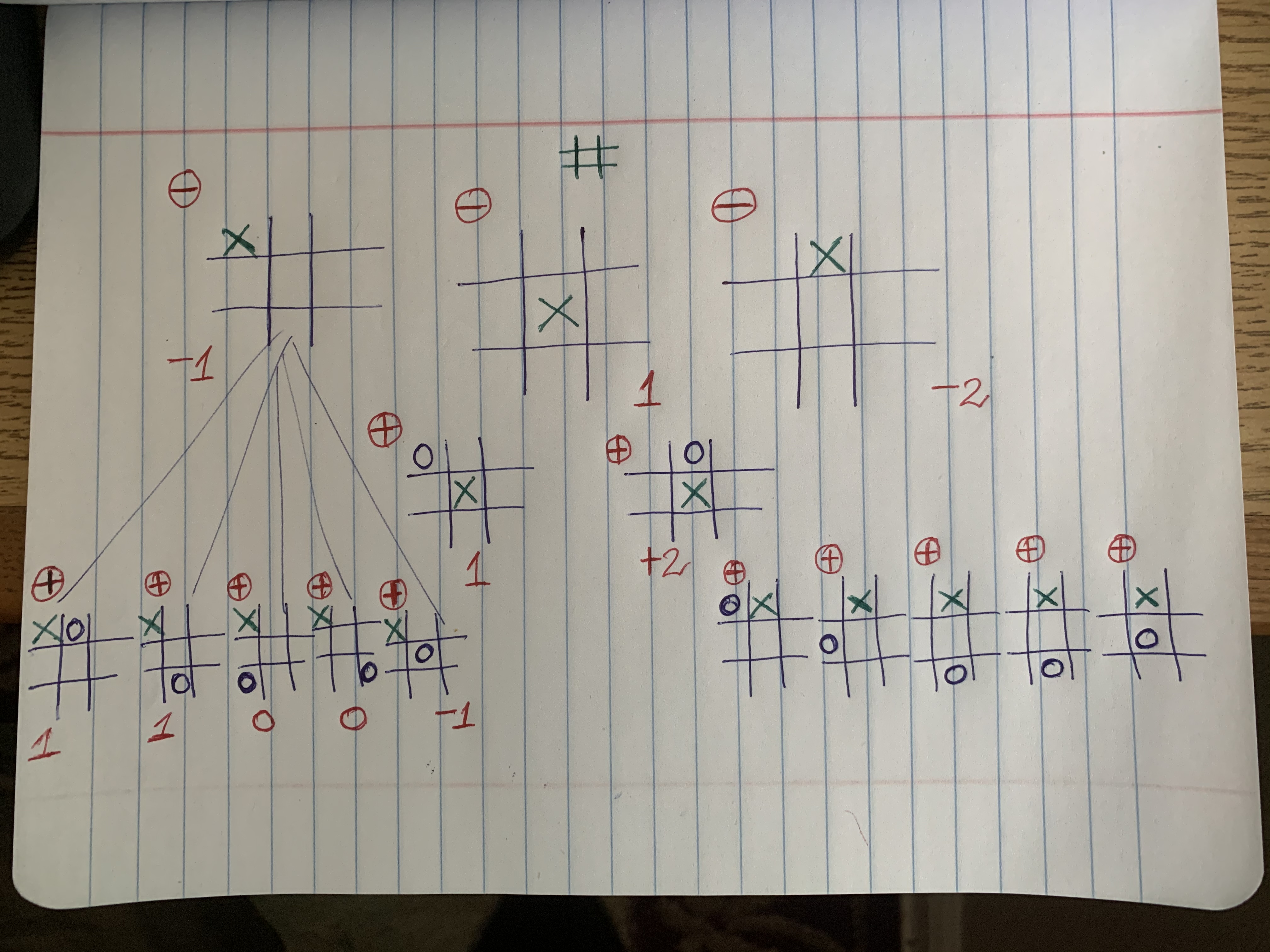
A Game Tree for a look ahead level of 2 is shown above. All other level are symmetric. The depth ‘d’ of the game tree is the max look ahead levels. Each board position is represented as a tree node. ‘+’ at nodes indicates that the maximizing player is about to make the move and ‘-‘ at the nodes indicates that the minimizing player is about to make the move. The best move for a player from a board position or node could be found by first constructing the game tree and applying the evaluation functions at the leaves as for leaves of look ahead level 2 shown above.

Now, the next step would be to move these values up the tree by assigning the min of the values of evaluation functions of all sons to a ‘-‘ node and the max to the ‘+’ node. For the above game tree at level 0, the player ‘+’ is to select any of these moves. We have moved up the min values to all the ‘-‘ nodes from their respective sons. As ‘+’ is maximizing player, he would certainly select the board position with the max value i.e the position with ‘X’ at the center of the board. Likewise the game proceeds. Such as a Game Tree node be represented as below –

struct treenode{
                int turn;
                int board[3][3];
                structure node * son;
                structure node * next;
};

typedef struct treenode * NODEPTR;