Depth First and Breadth First Traversal

Depth first traversal of a Graph could be used to traverse a directed or un-directed graph and thus creating a spanning tree. Depth first traversal is a pre-order traversal of the given graph or spanning tree. The traversal starts from a node and traverses along the path until it reaches a node which has no successors or a node of whose successors have been visited. It then resume to a node whose successors are not visited and then traverses the new path emanating from that node. Traversals are of the order O(N2) for adjacent rep and O(n+e) for linked graph representation, where e->edges.

Breadth first traversal visits all successors of a visited node before it visits the successors of any of those successors.

Consider the graph below –

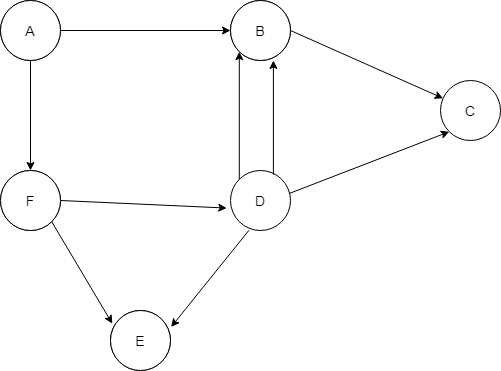
Here, Depth First Traversal  starts at node A. The pre-order traversal of the Graph thus yields A B C D E F which is represented as the following Spanning Tree –

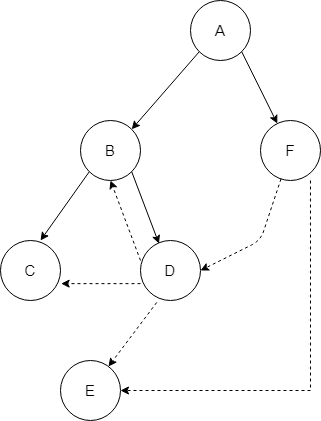
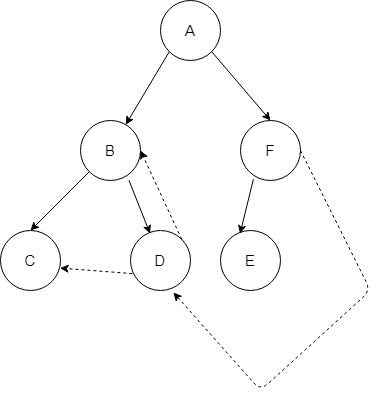
The Depth First Spanning Tree obtained after pre-order traversal (root, left, right) is ABCDEF.

Breadth First Traversal is of the order A B F C D E according to below Spanning Tree –