Minimal Spanning Trees and Kruskal’s Algorithm
July 7, 2020
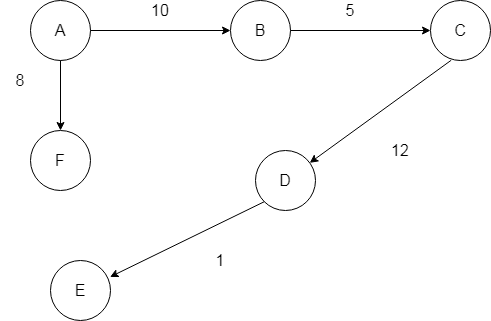
Given a weighted graph G, it is often desired to generate a spanning tree such that the sum of the weights of the tree edges is a minimum. Such a tree is called a Minimum Spanning Tree. Such a method is the cheapest way of connecting all nodes of G.
Kurskal’s Algorithm
Kurskal’s algorithm is a method to create Minimum Cost Spanning Trees from a given network. The min cost S.T is built edge by edge by selecting those edges first which have least cost(weight). Each edge is included only once. If there are n nodes in the network, there will be exactly (n-1) edges in the Minimum Cost Spanning Tree.
Consider the graph below –
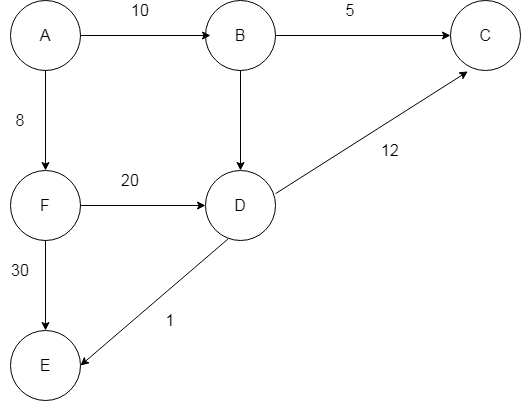
Applying Kurskal’s Algorithm, the resulting Minimum Cost Spanning Tree is as shown below –
About The Author
